Am 16.01.2024 fand der diesjährige Bolyai-Wettbewerb statt. Natürlich waren wie jedes Jahr Teams aus fast allen Klassenstufen vertreten, sogar in ihrer Mittagspause.
Aber was ist der Bolyai-Wettbewerb überhaupt?
Bei diesem Mathematik-Wettbeewerb dürfen Teams mit bis zu vier Personen mitmachen und sich spannenden Matherätseln stellen. Insgesamt 14 Aufgaben warten auf das Team und können innehralb einer Gruppe frei aufgeteilt oder auch zusammen gelöst werden. Für die Bearbeitung der Aufgaben steht dem Team eine ganze Stunde zur Verfügung.
Die teilnehmenden Teams messen sich in einer Gruppe mit den besten Teams aus Baden-Württemberg, Rheinland-Pfalz und dem Saarland.
Das schwierigste am Bolyai-Wettbewerb ist hierbei nicht die die Komplexität der Aufgaben sondern die Zeit, die möglichst effizient genutzt werden sollte. Hierbei haben wir in dem Team mit dem ich teilgenommen habe auf gute Absprache und individuelle Stärkeren gesetzt, wir haben also möglichst schnell versucht Aufgaben zu finden die uns potentiell besser liegen. Daraufhin haben wir angefangen die Aufgaben so schnell wie möglich zu bearbeiten. Hierbei musste man stets darauf achten sich nicht zu lange mit Aufgaben zu befassen um Zeitverschwendung zu vermeiden. Kam man also nicht weiter, teilte man dies den Teammitgliedern mit und befasste sich mit der nächsten Aufgabe.
Wie auch die letzten Male gab es auch dieses Jahr wieder besonders interessante und anspruchsvolle Aufgaben, wie beispielsweise die 3. Aufgabe der 11. Stufe dessen Aufgabenstellung wie folgt lautet:
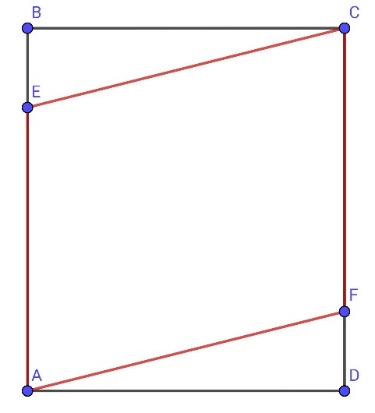
„Wir markieren auf den Seiten AB und CD des Rechtecks ABCD die Punkte E bzw. F so, dass die Figur AECF ein Rhombus (Raute) ist. Wenn die Länge von AB 16 cm und die Länge von BC 12 cm ist, wie lang ist dann die Strecke EF ?“
Unser Lösungsansatz:
Die Strecke AB und BC sind uns bekannt.
Wir können die Strecke AE mit der Länge x beschreiben.
Daraus folgt das die Strecke EB = AB – AE also EB = 16cm –x.
Nun kann man die Hypotenuse EB, die da bei einer Raute alle Seiten gleich lang sind EB = AE also x ist, aus dem Dreieck BCE berechnen mit den Strecken EB = 16cm – x und BC = 14cm.
Hierbei ergibt sich für jede der Seitenlänge der Raute x = 12.5cm.
Die Strecke EB = 16cm – 12.5cm = 3.5cm
Der vertikale Höhenunterschied zwischen F und E ist in diesem Fall also AE – EB : 12.5cm – 3.5cm = 9cm
Die Strecke EF lässt sich wieder als Hypotenuse mit dem Satz des Pythagoras berechnen, indem man den Höhenunterschied von E bis F und die Länge der Strecke BC als andere Seiten des Dreiecks verwendet.
Als Lösung erhält man nun 15cm für die direkte Strecke von EF.
 |
Für weitere spannende Aufgaben jeglicher Klassenstufen samt Lösungen kann die offizielle Website des Bolyai-Wettbewerbes https://bolyaiteam.de/ wärmstens empfohlen werden.
Wir möchten uns besonders beim Förderverein für die Übernahme der Startgelder bedanken.
Bericht: Len H., Fabian H. (J1)
Fotos: C. Gogollok



















